“I dream of instruments obedient to my thought and which with their contribution of a whole new world of unsuspected sounds, will lend themselves to the exigencies of my inner rhythm.” - Edgard Varese

Overview
Thought-Obedient Instruments (TOI) is a collection of unconventional synthesizers packed into a VST plugin.
It is a mix of experimental synthesis techniques and ideas that each may have varied levels of musical applicability, but in the end it is an experiment to see what might work.
Built from the ground up with JUCE.

Algorithm Implementation
Sampler
This is a traditional sampler that loads a file and allows speed-variable playback and truncation.
Hopper
This is the interface of a traditional sampler supplemented by the FFT/IFFT pipeline, allowing for deep control of the window hops, windowing, FFT order, and phase processing through the FFT/IFFT process.
Parameters:
- Hop Size: FFT Hop Size
- Hann Window: Scale of the Hanning window applied to amplitude over time before the FFT
- FFT Order: 2^(FFT Order) = FFT size
- Phase Process: Phase Processing method:
- 1 = Keep: Retain phase of the original sample across the FFT and IFFT.
- 2 = Zero: Align phases of all frequency bins.
- 3 = Disperse: Distribute frequency bin phases over a single cycle.
- 4 = Random: Randomly offset frequency bin phases from their original values.
- 5 = Zandom: Zero the frequency bin phases, then randomize them over a single cycle.
- PP Scale: Phase Processing scale. Controls the amount of randomization or dispersion.
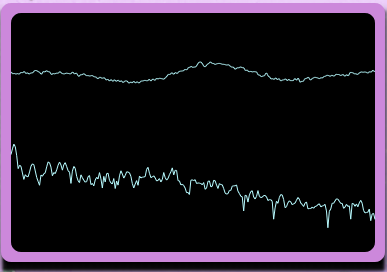
Parabolic Sine
This is a relatively simple sound source in which a spline of two quadratic functions is used to replicate a sine wave. The shape of the waveform is not precisely sinusoidal, so there are some harmonics present in the resulting signal. The implementation is very simple, just using the sample sine oscillator structure from the JUCE example code, but replacing calls to the standard sine function with calls to a quadratic spline function, containing two quadratic mathematical functions.
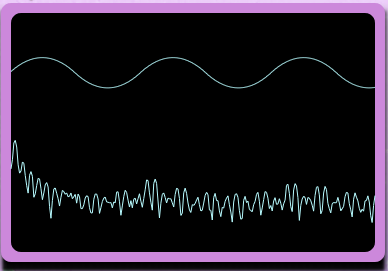
Fourier Scanner
This is, at its core, a modulatable Fourier transform of an input sample, translated back into the time domain as a sum of sine signals. The has control over the window span over frequency and time and the transform resolution. Ultimately, these parameters will be modulatable by other generators. By scanning through the input sample, the user can pick out different tones over the sample’s time or frequency. Short windows will generate sustained playable tones representing miniscule timbres only fleetingly present in the original sound.
This synthesis engine may “scan” by moving the Fourier transform window across the time domain, behaving as a series of overlapping STFT windows. This is similar to time-stretching, as described in DAFX. With modulation of the various parameters by other generator instances, this algorithm will likely generate some interesting musical tones.
The Fourier Scanner also features multiple methods of phase distortion, notated as “phase processing” in the interface. In the transformation process, frequency component phases can be preserved, zeroed, randomized by a user-specified degree, or distributed evenly.
This algorithm exposes most parameters of our FFT-IFFT pipeline, including:
- Time window position
- Time window size
- Frequency window position
- Frequency window size
- FFT/IFFT order
Parameters:
- T Min: Beginning of the time window, in samples
- T Size: Length of the time window, in samples
- F Min: Minimum of the frequency window in Hz
- F Size: Size of the frequency window in Hz
- Hann: Scale of the Hanning window applied to amplitude over time before the FFT
- FFT Order: 2^(FFT Order) = FFT size
- Phase Proc: Phase Processing method:
- 1 = Keep: Retain phase of the original sample across the FFT and IFFT.
- 2 = Zero: Align phases of all frequency bins.
- 3 = Disperse: Distribute frequency bin phases over a single cycle.
- 4 = Random: Randomly offset frequency bin phases from their original values.
- 5 = Zandom: Zero the frequency bin phases, then randomize them over a single cycle.
- PP Scale: Phase Processing scale. Controls the amount of randomization or dispersion.
Harmonic Highlight:

This serves as an amplitude window, or a two-way gate, on each FFT frequency bin. Amplitude boundaries of the gate are “soft,” scaling reduction relative to proximity to threshold. This process allows for isolation or removal of dominant frequencies in a signal. This can be useful for noise reduction and creative sound design.
Parameters:
- Hop Size: FFT Hop Size
- Hann Window: Scale of the Hanning window applied to amplitude over time before the FFT
- FFT Order: 2^(FFT Order) = FFT size
- Phase Proc: Phase Processing method:
- 1 = Keep: Retain phase of the original sample across the FFT and IFFT.
- 2 = Zero: Align phases of all frequency bins.
- 3 = Disperse: Distribute frequency bin phases over a single cycle.
- 4 = Random: Randomly offset frequency bin phases from their original values.
- 5 = Zandom: Zero the frequency bin phases, then randomize them over a single cycle.
- PP Scale: Phase Processing scale. Controls the amount of randomization
- Min: Minimum frequency bin amplitude
- Max: Maximum frequency bin amplitude
- Scaling: Amplitude reduction above/below threshold, relative to previous amplitude proximity to threshold.
Mr. Shifty

Mr. Shifty allows for frequency-domain shifting or stretching of frequency bins. This effect can range from a clean pitch shift to a complete restructuring of a sound’s harmonic content.
Parameters:
- Hop Size: FFT Hop Size
- Hann Window: Scale of the Hanning window applied to amplitude over time before the FFT
- FFT Order: 2^(FFT Order) = FFT size
- Phase Proc: Phase Processing method:
- 1 = Keep: Retain phase of the original sample across the FFT and IFFT.
- 2 = Zero: Align phases of all frequency bins.
- 3 = Disperse: Distribute frequency bin phases over a single cycle.
- 4 = Random: Randomly offset frequency bin phases from their original values.
- 5 = Zandom: Zero the frequency bin phases, then randomize them over a single cycle.
- PP Scale: Phase Processing scale. Controls the amount of randomization
- Shift: Frequency bin offset
- Spread: Frequency bin spread / pinch
Spline Generator

This generator approximates a spline-driven waveform to match 10 coefficients. This allows the user to “draw” a waveform and hear an interpolated rendition of their wave.
Parameters:
- C[x]: Coefficient value x
Interpolating Spline
This generator makes a waveform by calculating a 1-dimensional B-spline curve. The spline’s control points are chosen by sampling points in a source waveform, meaning this generator acts as a pseudo-interpolation of a source wave. The output does not match up with the source exactly, but attempts to recreate the general shape of it. There is also a version of the spline generator that allows the user to just make their own spline by setting the spline control points manually.
Parameters:
- Point Density